编者按
在新型电力系统建设过程中,新能源比例不断提升。由于新能源的不确定性、波动性等特点,电力系统需要足够的灵活性资源来保障电力供需平衡和系统安全稳定,而其中重要的一个环节就是来自需求侧的灵活性资源。在国内的用电结构中,工业用户用电占比高达66%,与商业、居民等类型用户相比,工业用户具有用能容量大、用能逻辑性强等特点,通过调整生产计划、启停设备等方式响应电网的调控信号,充分调用其生产中的灵活性空间,能够有效支持电力系统的稳定运行。《中国电力》2024年第1期刊发了苏湘波等人撰写的《基于负荷台阶的工业需求响应用户优选方法》一文。文章首先提出了负荷台阶的数学概念,并给出了相应的数据处理方法;然后根据用户日前15天的历史负荷数据,提出了基于负荷台阶的工业用户需求响应潜力评估的指标体系,采用逼近理想值排序法(technique for order preference by similarity to ideal solution,TOPSIS)建立了用户优选模型,从3个时间维度进行需求响应潜力量化;最后采用k-means聚类和近邻传播算法实现用户优选。

摘要
在未来高比例新能源渗透下,供需平衡不确定性逐步增加,需求响应是通过挖掘用户侧灵活性资源保障系统电力电量平衡的重要手段。在电力部门进行需求响应工作时,需要使用历史数据来初步评估负荷响应潜力,以便选择潜力高的用户并展开动员工作。面向表征工业用户用能特点的负荷台阶,对其进行了定义并给出了数学表达,进而提出了基于负荷台阶的工业需求响应用户优选方法。首先,构建了基于负荷台阶的工业用户多时间尺度需求响应潜力指标体系;然后,构建了需求响应用户优选模型,实现对不同用户响应潜力的初评估,并利用k-means算法和近邻传播算法进行群体划分,在不同时间尺度对用户进行优选;最后,基于水泥、造纸等4个行业的多个工业用户实际负荷数据进行算例分析,呈现了所提方法下工业需求响应的用户优选结果。

负荷台阶可以准确描述用户的相对稳定状态,台阶之间的负荷量之差可以反映用户的可调节潜力。需要说明的是,可调节潜力是在生产流程中由于用能变化产生的理论潜力。本章提出负荷台阶的数学定义,并给出负荷台阶信息矩阵的提取算法。
1.1 负荷台阶数学定义
负荷台阶是指在用户的日负荷曲线中一段超过1 h以上的局部变化率低于某一数值的稳定负荷。
局部变化率α为
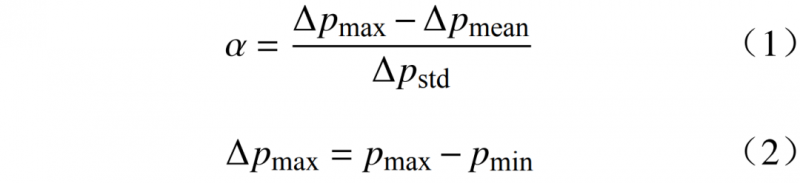
式中:p为局部负荷;
通常取α<3作为台阶的判断条件。如图1所示,日前15天以1次/(15 min)的采样频率的负荷差分值的分布是近似服从高斯分布的。负荷台阶代表这段时间内的负荷在一个稳定的范围内波动,而当它的波动范围
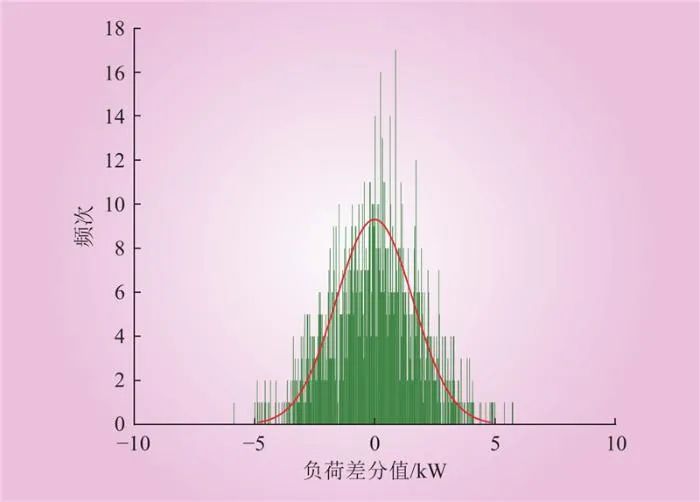
Fig.1 Distribution of load difference values for the previous 15 days
对负荷台阶的识别,在数学上是指在处理负荷数据时只保留负荷台阶的稳态信息,舍弃负荷台阶之间的暂态信息。对于保留的稳态信息,记录这段负荷台阶的平均值、起始时间和结束时间。对于舍弃的暂态信息,可以通过负荷台阶之间的高度差和转换时间进行近似处理。负荷台阶示意如图2所示。
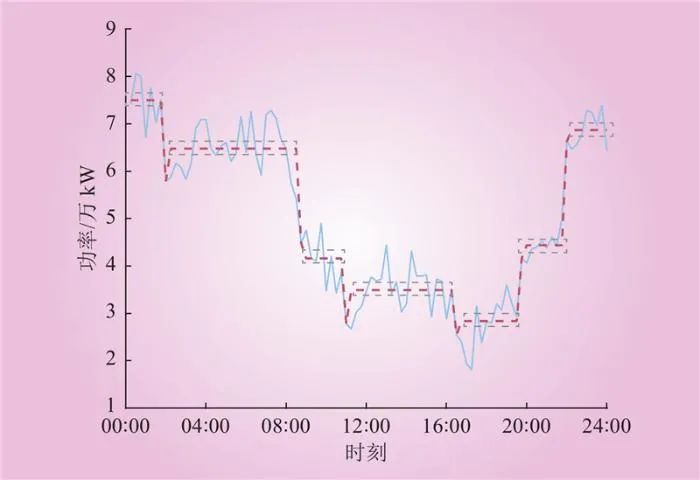
Fig.2 Schematic diagram of load step effect
图2中浅蓝色实线代表的是某用户某日以1次/(15 min)的采样频率实际日负荷曲线,红色虚线代表的是经过负荷台阶处理过后的日负荷曲线,灰色虚线框标注的是负荷台阶。由图2可知,负荷台阶可以有效记录稳态信息,去除台阶内不必要的负荷波动,从而减少冗余信息。
1.2 负荷台阶提取流程
以采样频率为1次/(15 min)的日前15天的日负荷数据为例,通过对日负荷曲线中所有的数据进行遍历,找出所有的台阶。具体步骤如下。1)定义初始数组和判断条件。定义一个候选台阶数组a,用于存储初始的4个负荷值。使用局部变化率α<3作为负荷台阶判断条件。
![]()
2)遍历历史负荷数据W,识别负荷台阶。遍历方式为
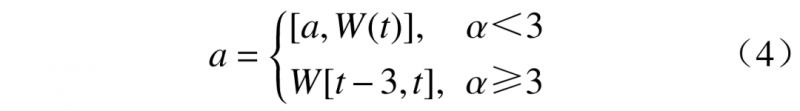
根据式(4)对a进行更新。其中t的初始值为5,代表的是遍历的最新位置。t的更新方式为:①若
3)记录被识别的第i个负荷台阶的信息Pj(i)
![]()
式中:pj,1(i)、pj,2(i)和pj,3(i)分别为存储负荷台阶的原历史负荷数据的平均值、起始时间和结束时间;ni为整个日负荷曲线中被识别的台阶数量。日前第i天日负荷曲线的台阶信息矩阵Ti为
![]()
综上,日前15天的负荷台阶信息矩阵T为
![]()

面向需求响应的工业负荷潜力指标体系是建立在实时削峰、日内移峰、日前调峰3个维度上的,是实行工业需求响应用户优选的基础。其中实时削峰潜力指在电网紧急情况下,电力公司于需求响应执行前30 min,通过平台向参与主体下发调节指令,告知响应范围、需求量、时段等信息,用户能参与实时需求响应实现削峰的能力大小。实时削峰潜力可以从可削减的负荷、响应所需的时间、用户高峰负荷出现的灵活程度3个维度来量化。日内移峰潜力指用户参与约时需求响应在日内通过可平移负荷实现削峰填谷的潜力大小。日前调峰潜力指用户可以合理调节生产计划,分配休息日与工作日,实现休息日与工作日之间的负荷平移潜力。从实时、日内和日前3个时间尺度,对工业用户参与需求响应做了潜力量化,构成了面向需求响应的工业负荷潜力指标体系。相较于目前已经提出的指标体系,本文在实时削峰潜力方面,基于负荷台阶的切换时间提出了主阶响应时间这一指标,而以往的负荷数据指标却很难描述该特征,响应时间是实时响应需要着重考虑的因素,这也是采用负荷台阶构建指标体系的优点所在;在日内移峰潜力方面,负荷台阶将随机性较强的峰谷负荷用代表性更强的最高负荷台阶和最低负荷台阶代替,使得对应的日内可平移负荷更为可靠;在日前调峰潜力方面,基于负荷台阶计算了高负荷日和低负荷日之间的可调峰负荷和分布情况,可较好地反映其日前潜力。
2.1 实时削峰潜力
实时削峰潜力从参与削峰的负荷量、峰值负荷的灵活削减程度和响应削峰需求所用时间3个角度进行刻画。
2.1.1 主次削减负荷γ1
日负荷曲线中最高的负荷台阶称为主阶,主阶旁边的两个台阶称为次阶,主阶与次阶之间的最大差值就称为主次削减负荷。主次削减负荷值越大,说明用户参与实时削峰的可实现潜力就越大。考虑15天内主次削减负荷的平均值,主次削减负荷公式为
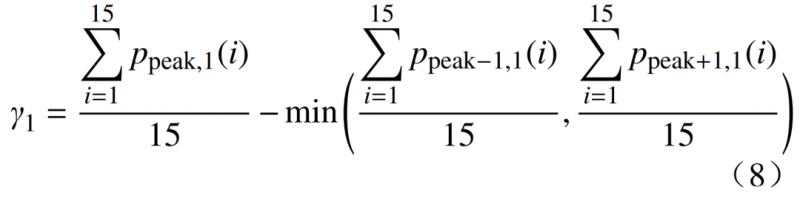
式中:p
2.1.2 主阶灵活性负荷γ2
峰值灵活性负荷指的是主阶负荷值在15天内的标准差,该值越大说明阶的灵活性越强,用户参与实时削峰的潜力越大。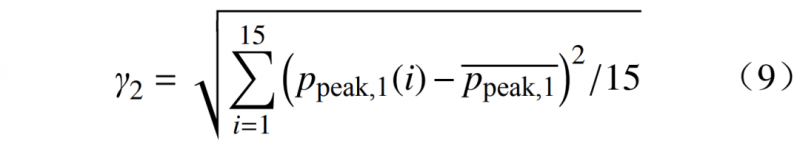
式中:为15天内p
2.1.3 主阶响应时间γ3
主阶响应时间指的是主阶负荷削减所需要的时间,即往两侧台阶转换所需要的时间,主阶响应时间越小,代表用户参与实时削峰的潜力越大。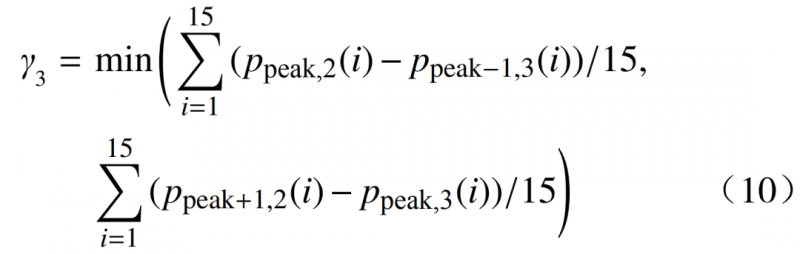
式中:p
2.2 日内移峰潜力
日内移峰潜力从用户的日内可平移负荷量、进行移峰的可靠性和以及负荷台阶出现的灵活性3个角度进行刻画。2.2.1 日内可平移负荷γ4
对于参与日内移峰用电的工业用户,采用15天以来每日的主阶负荷减去每日负荷台阶的最小值的平均值作为其日内可平移负荷的大小,其值越大就代表该用户日内移峰用电潜力越大。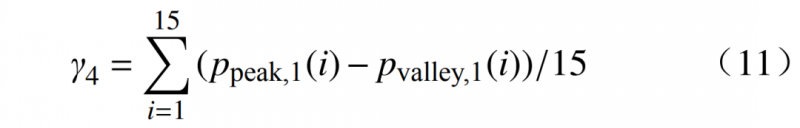
式中:p
2.2.2 日内峰谷差率γ5
日内峰谷差率是15天内峰谷平均值的差与峰值的比值,其值越大说明进行移峰的可靠性越强,对应的潜力也就越大。
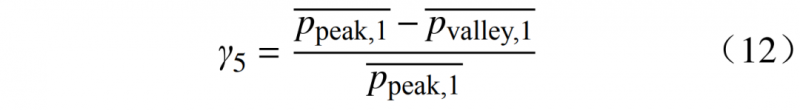
式中:![]() 代表
代表
2.2.3 台阶波动率γ6
台阶波动率指的是用户在日前15天内所有负荷台阶的高度组成的数列的方差除以均值,台阶波动越大,说明负荷可平移的潜力越大。
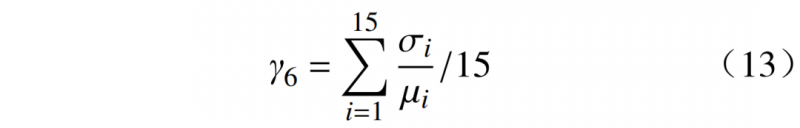
式中:σi、μi分别为第i天经过加权的负荷台阶高度的方差值、均值。每个台阶高度的加权值取决于该台阶的持续时间占该日所有台阶的持续时间的比例。
2.3 日前调峰潜力
日前调峰潜力从用户调节生产计划的日间可调峰负荷量、高峰负荷日出现的比例和日间负荷水平的灵活性3个角度进行刻画。2.3.1 日前可调峰负荷γ7
日前可调峰负荷用15天的负荷台阶化后每日平均负荷μi中的最大值与最小值之差来表示,其值越大,说明用户日前调峰潜力越大。其公式为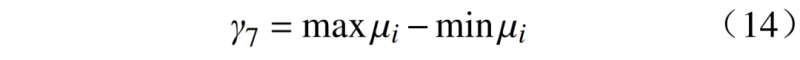
2.3.2 日前负荷率γ8
日前负荷率越大,说明可以参与调峰的潜力越大,其公式为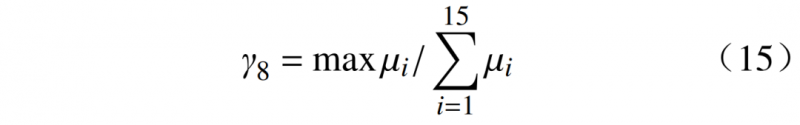
2.3.3 日前负荷散度γ9
计算每日负荷台阶的平均值的散度,该值越大,说明负荷分布越分散,随着天数的变化比较大,可以参与调峰的潜力也越大。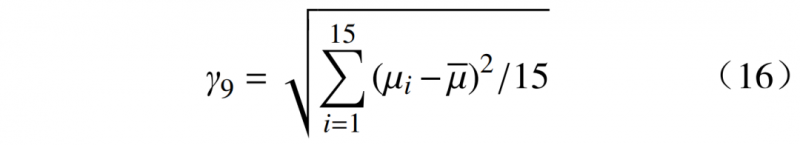
式中:
2.4 特征指标权重配置
要准确评定不同指标在潜力量化中的作用和贡献,需要对不同的指标配置不同的权重。权重是各个指标贡献大小的度量参数,可以反映指标之间的独立性和变异程度。通常有主观赋权和客观赋权两种方法。为了从客观角度对不同的潜力指标进行综合排序,本文采用熵权法进行权重配置。熵权法是一种客观赋权方法,根据各项指标的变异程度来确定指标权数,反映指标的信息量和重要性,广泛应用于输电网规划、电能质量评估和机组运行评价等领域,具有客观、适用性强和精度高的优点。具体步骤如下。1)欧几里得归一化。将每个指标缩放到单位长,可以使得每个特征向量的长度相同,从而消除不同特征之间的量纲差异,使得它们在计算相似度或距离时具有相同的权重。
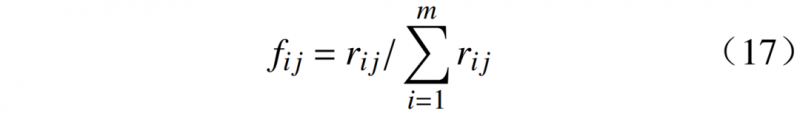
式中:fij为第j个指标下第i个被评对象的贡献度;rij为实测数据;i=1,2,⋯,m;j=1,2,⋯,n。2)计算熵值hj。熵值越小,说明指标的变异程度越大,提供的信息量也就越多,在综合评价中起的作用越大,则该指标的权重也应越大。如果某项指标的值全部相等,则该指标在综合评价中不起作用。
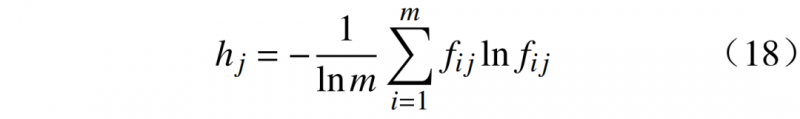
式中:hj为第j个指标的熵值;i=1,2,⋯,m;j=1,2,⋯,n。3)计算熵权ωj。当同类指标差异较小时,传统熵权计算方法误差较大,基于指数函数进行修正,可表示为
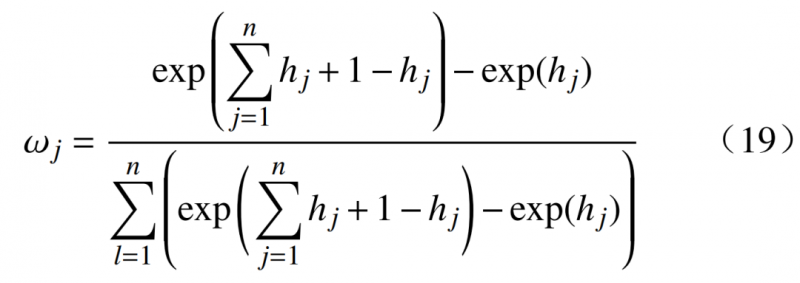
4)求出对应特征向量的权重。
![]()

量化由多个指标确定的综合潜力值,需要计算不同的指标的重要性,并保证不同的潜力量化结果处于同一维度,得到综合的客观评价。本文采用熵权法确定多指标的客观权重,利用TOPSIS法对用户的需求响应潜力进行量化评估,并采用k-means算法和近邻传播算法识别工业用户的群体分布,实现用户在多个响应潜力指标上的排序和在整个用户群体中的定位。
3.1 参数初始化
3.1.1 构建初始潜力矩阵
首先,设定实时削峰潜力为D1,日内移峰潜力为D2,日前调峰潜力为D3,用户集C=[c1,⋯,ci,⋯,cm],有m个用户;特征向量
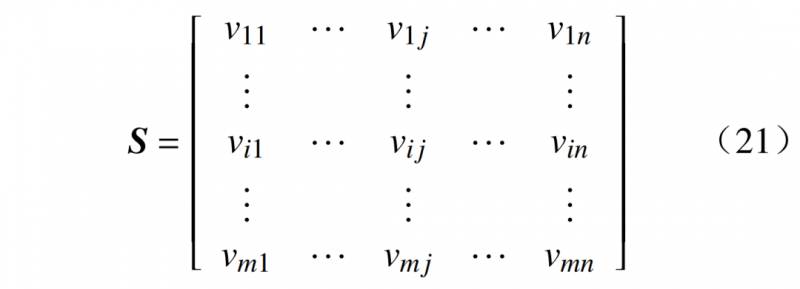
式中:vij为用户i的第j个指标的值。初始潜力矩阵作为需求响应量化潜力模型的数据基础,同时也为用户优选提供数据支撑。
3.1.2 指标值预处理
由于不同的指标量纲不同,不同的用户之间负荷水平存在数量级的差距,为了避免导致量化误差,需要对指标值进行如下处理。1)负荷归一化。在提取负荷台阶信息之前,对负荷归一化以避免后续指标中用户量级导致的量化误差。
式中:
p0代表用户日前15天的负荷;
2)量纲归一化。将vij归一化后变成yij,从而消除指标间的量纲。
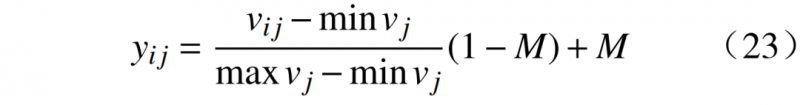
式中:i=1,2,⋯,m;j=1,2,⋯,n;M通常取0.25~0.75。
3)单位范数归一化。
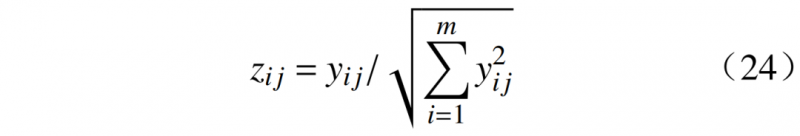
通过单位范数归一化可以消除不同用户之间的量纲差异,减少噪声和异常值的影响。
3.1.3 熵权法权重配置
针对不同的潜力,Dk(k∈1,2,3)对每个处理后的潜力矩阵进行权重配置,得到合理分配权重的加权潜力矩阵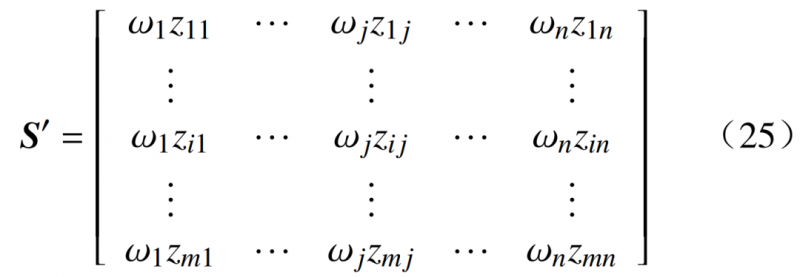
3.2 基于TOPSIS法量化排序TOPSIS法是一种根据评价对象与理想化目标的接近程度进行排序的距离综合评价方法,能精确反映各评价用户之间潜力的差距,具有较强的实用性和通用性。具体来说,TOPSIS法是一种多属性决策分析方法,其基本思想是选择一个最接近正理想解并且最远离负理想解的用户作为最有潜力的用户,使用相对接近度作为衡量潜力大小的参数。具体步骤如下。
1)确定正理想解和负理想解,分别是各属性值最大和最小的组合。除了主阶响应时间以最小值作为正理想解,其余均选择最大值作为正理想解。相反,则可得负理想解。
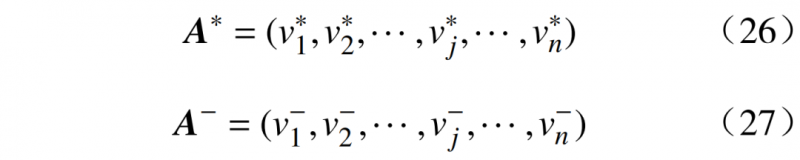
式中:
2)计算每个方案到正理想解和负理想解的距离,使用欧几里得距离度量。
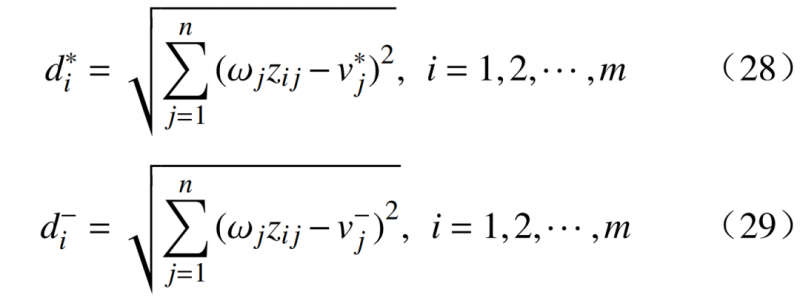
式中:![]() 分别代表用户
分别代表用户
3)计算每个方案的相对接近度,即到负理想解距离与到正理想解距离之和的比值。根据相对接近度对各方案进行排序,相对接近度越大,排名越靠前。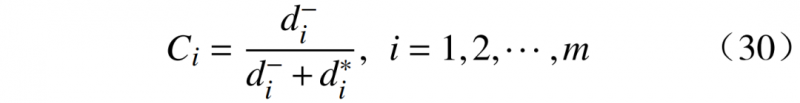
综上,能得到3类潜力量化矩阵,即参与需求响应的用户集C的实时削峰潜力矩阵![]() 日内移峰潜力矩阵
日内移峰潜力矩阵![]() 日前调峰潜力矩阵
日前调峰潜力矩阵![]() 从而得到用户的综合潜力矩阵D为
从而得到用户的综合潜力矩阵D为
![]()
然后根据用户在各个潜力上的相对大小,就能对用户的响应潜力进行排序。用户优选不仅要确定用户在潜力上的排序,而且还需要对整个用户群体进行合理的划分。本文采用k-means算法和近邻传播算法进行群体划分。其中k-means算法对单个潜力矩阵(
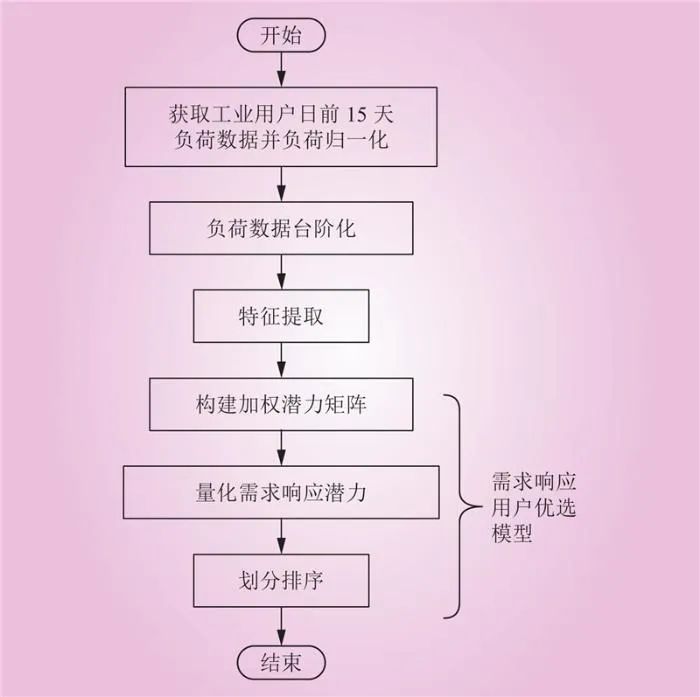
Fig.3 The industrial user preference process flowchart

基于某省份某一地区的水泥、造纸、铝冶炼和石油开采4个行业实际用户数据,本算例抽取48个连续15天的用户负荷数据作为样本,用户编号从1~48,以1次/(15 min)采样频率进行分析。其中编号1~13的用户来自水泥行业,编号14~25的用户来自造纸行业,编号26~39的用户来自铝冶炼行业,编号40~48的用户来自石油开采行业。算例分析的流程如下。
1)负荷数据台阶化。负荷台阶的判断条件取α<3,提取用户每天的负荷台阶,得到每个用户日前15天的台阶信息矩阵。
2)特征提取。计算每个用户的各类潜力指标,得到需求响应综合评价模型中所需要的初始值。
3)参数初始化。对数据进行去量纲化和权重配置。取M=0.6,得到的权重配置参数如下:实时削峰潜力γ1、γ2、γ3的权重分别为0.4471、0.3305、0.2224;日内移峰潜力γ4、γ5、γ6分别为0.3320、0.3561、0.3119;日前调峰潜力γ7、γ8、γ9分别为0.3933、0.2644、0.3423。
4)用户优选。分别对3种类型的潜力进行量化计算,得到最终的需求响应潜力综合数值进行优选。
4.1 工业用户需求响应潜力优选不同的行业之间需求响应潜力由于生产方式有很大的不同,行业内部的用户由于生产规模也有很大的不同,用户在一年不同的时间段由于生产计划也存在区别。对48名用户的潜力值由大到小降序排列,并采用k-means算法进行一维聚类,聚类数目为3,划分为高潜力、中潜力和低潜力行业。结果如图4所示。
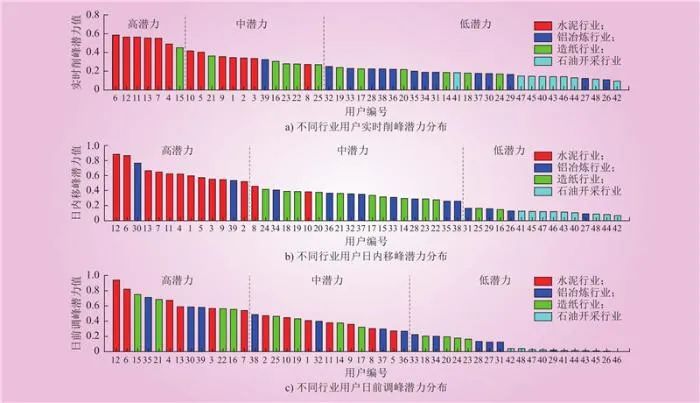
Fig.4 Quantification of user potential by different categories
在实时削峰潜力的聚类结果中,高潜力量化值大于等于0.4494,中潜力量化值在[0.2704, 0.4166]区间,低潜力量化值小于等于0.2517。在日内移峰潜力的聚类结果中,高潜力量化值大于等于0.5196,中潜力量化值在[0.2603, 0.4589]区间,低潜力量化值小于等于0.1660。在日前调峰潜力的聚类结果中,高潜力量化值大于等于0.5393,中潜力量化值在[0.2677, 0.4864]区间,低潜力量化值小于等于0.2258。由图4可知,用户12为典型的高潜力用户,用户46为典型的低潜力用户。通过绘制用户15天内的负荷曲线,对日平均负荷最大和最小的负荷曲线进行了加粗,并将两条曲线进行了负荷台阶化,分别用浅红色细线和黑色细线区分,如图5所示。用户12是水泥行业的用户,从日平均负荷最大曲线可知,峰时负荷可中断性强,切负荷时间相当短,近似为一条倾角90°的直角,说明削峰负荷大且切换时间短,符合实时削峰潜力强的负荷特性;从日内移峰的角度来说,其整个负荷曲线呈现高负荷、低负荷两阶梯的形态,且两段时间相当,说明日内可平移负荷容量大,符合日内移峰潜力高的负荷特性;从日前调峰的角度来说,其低负荷日和高负荷的负荷差距大且低负荷的天数占到总数的2/3,可以配合电网需求进行生产计划的灵活调整,符合日前调峰潜力强的负荷特性。同时,从低潜力代表用户42的负荷曲线分析,用户42是石油开采行业的用户,日内的负荷水平波动小,整体负荷率较高,日间的最大负荷和最小负荷差距也很小,因此用户42的负荷可调性弱,故而其实时、日内和日前的潜力都为低潜力。
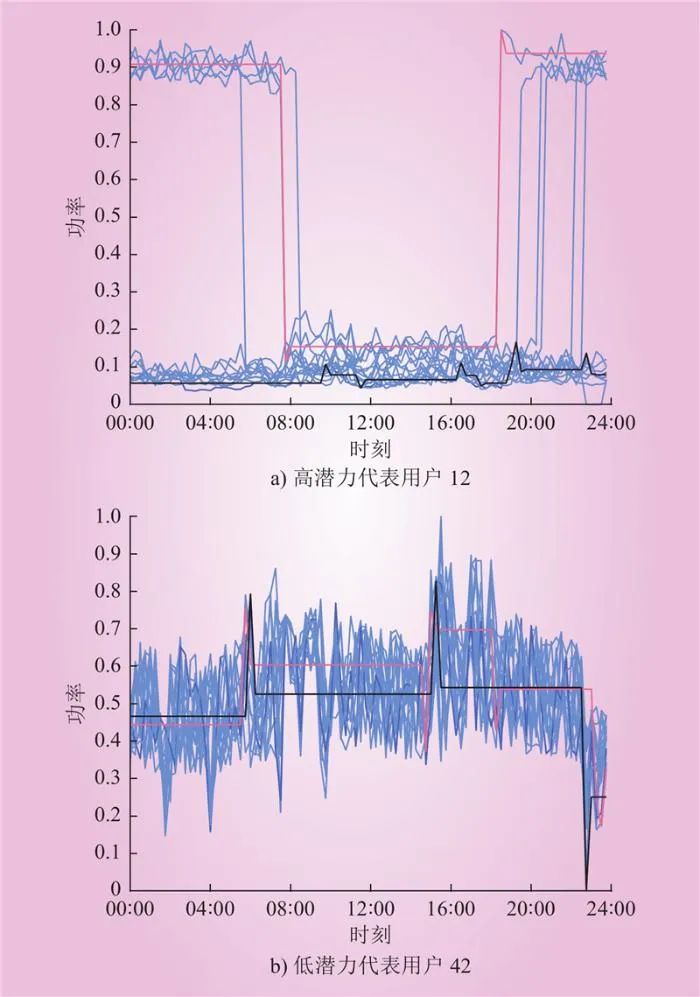
Fig.5 Load curves of users with high and low potential
通过对不同时间尺度下用户需求响应能力的划分和排序,能够为电力部门提前遴选高潜力的需求响应用户提供有效支撑,有助于其制定更适合的需求响应策略。4.2 工业负荷响应潜力群体识别对各行业用户潜力值取平均后,得到4个行业用户的综合潜力对比如图6所示。水泥行业在实时削峰潜力、日内移峰潜力和日前调峰潜力上都是最强的,而石油开采行业这3项潜力都是最差的;而造纸行业的日前能力较强,其余比较一般;铝冶炼的日内移峰能力较强,日前调峰潜力较弱,比较符合当下的行业共识。
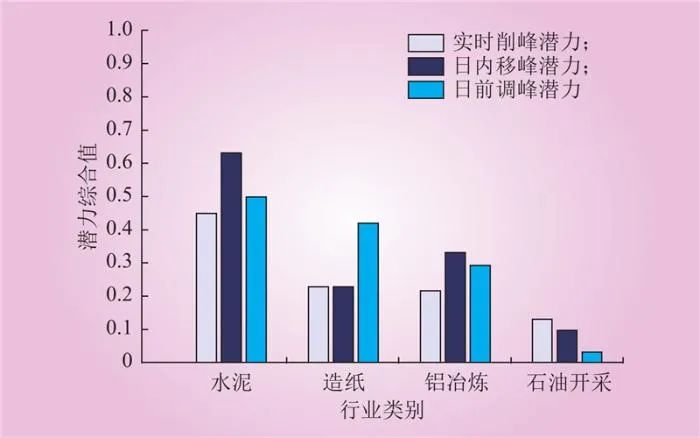
Fig.6 Comparison of comprehensive potential among different industries
基于求得的需求响应综合量化潜力值,使用近邻传播算法进行工业用户群体识别,得到48个用户的聚类结果如图7所示。
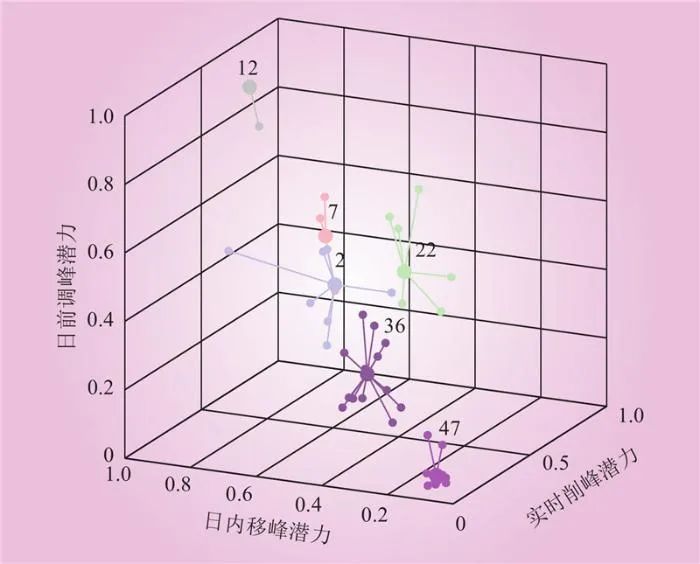
Fig.7 Identification of industrial user groups
由图7可知,通过近邻传播算法聚类之后,将近邻传播算法自动聚成了6类,同类别用户需求响应潜力特征相似度高共性特征明显且差异性小,聚类中心分别是用户2、用户7、用户12、用户22、用户36和用户47。6类群体代表用户潜力值和15天的负荷曲线如图8~9所示。
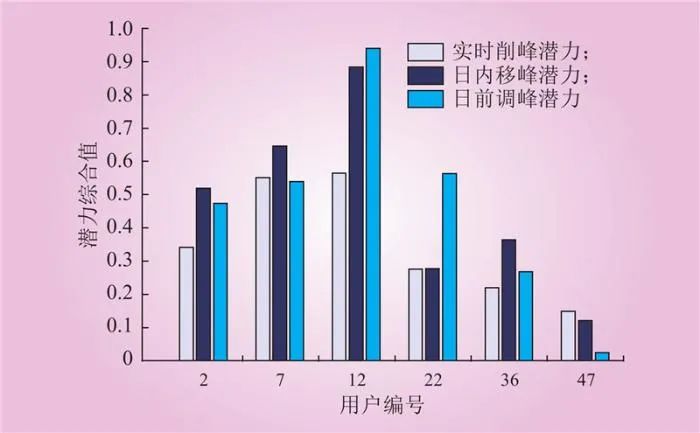
Fig.8 Six categories of groups represent user potential values
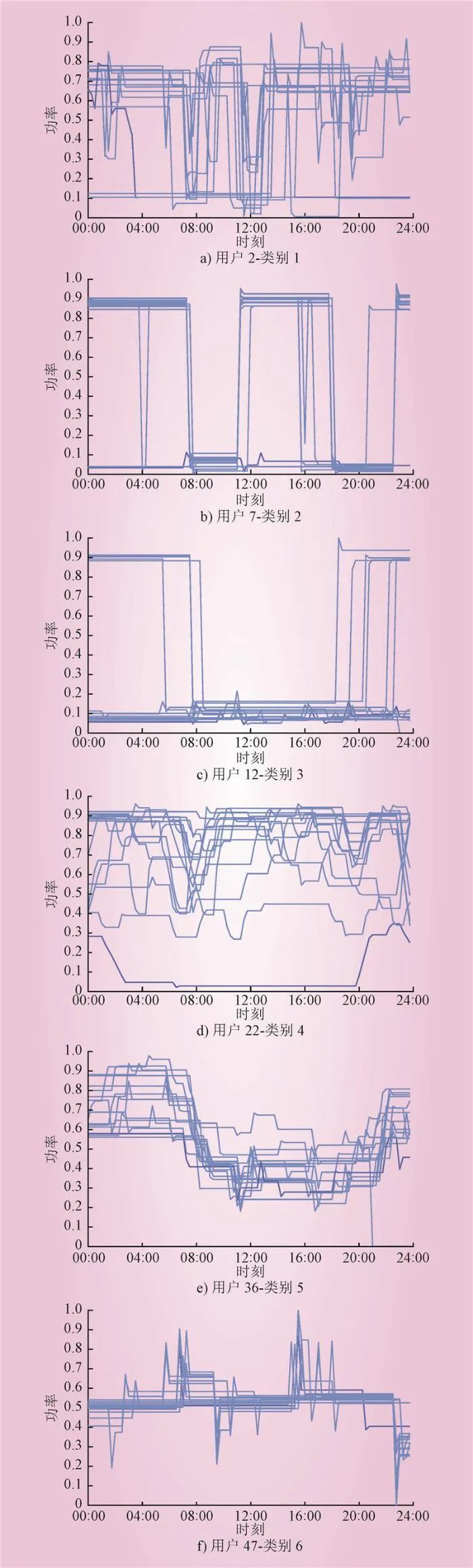
Fig.9 Load profile of groups represent user of six categories for fifteen days
由图8和图9可知,类别2、3的用户群体整体表现为高潜力,实时削峰潜力、日内移峰潜力和日前调峰潜力都是高潜力;而类别6的用户的3类潜力均为低潜力。由图10行业用户聚类结果的分布可知,类别2、3均只含水泥用户,类别6以石油开采行业用户为主,符合水泥用户高响应潜力、石油开采因负荷稳定性好而响应潜力弱的特点。
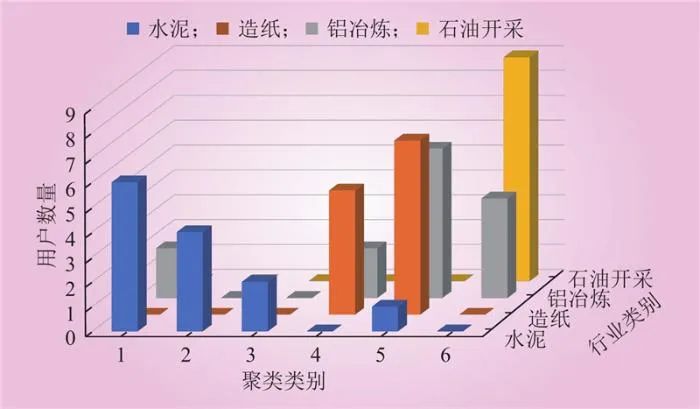
Fig.10 Distribution of user clustering results by different industries
特别地,由图9可知,不同类别聚类中心之间的负荷曲线轮廓相似度小,负荷特性差异大,不同类别之间行业用户的分布也具有显著差异,说明了基于负荷台阶的特征体系在群体识别的有效性、科学性,同时管理侧也可以根据不同行业的潜力特点、不同群体各类潜力的高低对整个群体进行优选,开展合适的需求响应策略。
算例结果表明,本文提出的方法可以在仅使用历史负荷数据的情况下,从多时间尺度刻画用户响应能力,准确区分不同行业间的负荷特性,有效地实现潜力评估和群体划分,可以帮助负荷聚合商和电网调度中心在不同场景的需求下实现用户优选,助力需求响应的大规模推广。

本文针对在工业用户推广需求响应时数据有限、面向范围广的特点提出了一种基于负荷台阶的优选方法。本文给出了负荷台阶的数学定义及其提取方法,能同时对多种类型的工业用户进行分析,而不仅仅只局限特定类型的用户;能从实时、日内和日前3个角度分析用户响应潜力,适用于更多场景;所用方法考虑用户隐私,不需要响应数据和内部模型数据,仅使用日前15天历史负荷数据可实现工业需求响应的用户优选。基于负荷台阶的需求响应潜力指标体系,采用TOPSIS法从实时削峰潜力、日内移峰潜力和日前轮休潜力对工业用户参与需求响应的潜力进行了量化。采用近邻传播算法对工业用户参与需求响应的能力进行了群体识别。算例通过对水泥、造纸等4个行业48名用户15天的数据进行潜力评估,能有效分析用户的用电行为模式,通过负荷台阶的高低落差来计算可控调节潜力,台阶转换时间计算响应时间,从实时、日内和日前的角度量化评估不同用户参与需求响应的可靠调节能力,在多个场景的需求下实现用户优选,为需求响应的大规模推广提供了有效的支撑。




